Red-Black tree는 MIT OCW 강의에서 다루지 않았지만 AVL트리를 공부하다 보니 사실상 AVL트리는 쓰이지 않고 Red-Black Tree나 B-tree, Treaps 같은 구조를 쓴다는 이야기를 듣고 호기심에 찾아본 트리이다. 한번도 사용해 보지 못한
enum을 사용하고 이름도 독특해서 레드블랙 트리를 공부해 보기로 했다.Introduction to Algorithms 을 참고하였다.
Red-Black Tree
레드블랙 트리는 AVL 트리와 마찬가지로 최악의 경우에도 height를 $log_2n$으로 유지하는 트리이다. AVL의 경우 Balanced여서 탐색은 빨리 수행할 수 있었지만 새로운 데이터를 삽입하거나 삭제하는 경우 AVL의 성질을 유지시키기 위해 많은 연산이 필요하였다. 레드블랙 트리는 좀 더 유연하게 balanced를 유지하여 AVL트리 보다 삽입과 삭제가 더 용이하다.
Properties
레드블랙 트리는 BST의 구조에서 color가 추가되어 모든 노드는 Red나 Black를 갖고 있으며 이는 거의(approximately) balanced인 상태를 유지시키기 위해 활용된다.
각각의 node는 color, key, left, right, parent 를 갖고 있으며 부모 노드나 자식 노드가 없을 경우 NIL을 가리킨다.
정리하면 Red-Black Tree는 다음과 같은 성질을 갖고 있다.
- 모든 노드는
red이거나black이다. root노드는black이다.- 모든
leaf(NIL)는 black이다. - 만약 한 노드가
red이면 자식 노드(들)은black이다. - 각각 노드에서, 그 노드로부터 leaves 까지의 simple path들은 같은 수의
black노드를 지난다. (root노드에서 가장 아래 까지(leaf 노드들 까지) 어느 경로로 내려가도 같은 수의black노드를 만나며, 꼭root노드일 필요 없이 어떤 노드를 선택해도 그 노드로부터 끝까지 내려가면서 만나는black의 수는 같다. )
이러한 조건을 만족하면 다음과 같은 명제를 만족한다.
$n$ 개의 노드를 갖고 있는 Red-Black Tree는 최대 $2lg(n+1)$ 의
height를 가진다.증명)
어떤 노드
x에서x를 제외하고leaf까지 가면서 만나는black노드의 수를 black-height of the nodex라고 하고 $bh(x)$ 라 쓰자.Claim) 어떤 노드
x를root로 갖는 subtree는 최대 $2^{bh(x)}-1$ 개의 노드를 갖고 있다.$x$ 의 높이를 이용해 귀납법을 통하여 증명하자.
만약 $x$ 의 높이가 0이면, $x$ 는 항상
leaf(NIL)이며 따라서 $x$ 의 서브트리가 갖는 노드의 수는 최대 $2^{bh(x)}-1 = 2^0-1 = 0$ 개 이다.이제 노드 $x$ 의 높이가 어떤 양수 $k$ 이고 두 자식 노드를 갖는다고 해보자. 이 두 자식 노드는
red인지black인지에 따라 $bh(x)$ 와 $bh(x)-1$ 의 black-height를 지닐 것이다. $x$ 의 자식 노드의 높이는 $k-1$ 이고 claim에 따라 이 자식 노드들의 subtree는 최대 $2^{bh(x)-1}-1$ 개의 노드를 갖고 있다.따라서 $x$를 root로 갖는 subtree는 최대 $(2^{bh(x)-1}-1 +(2^{bh(x)-1}-1) + 1 = 2^{bh(x)}-1)$ 개의 노드를 갖고 있다.$\blacksquare$
이제 $h$ 를 트리의 높이라고 해보자. 위 Property 4에 의해
root부터leaf까지 이동하는 simple path에서root를 포함해 최대 절반의 node들은 black이다. 즉,root노드의 black-height는 적어도 $h/2$가 된다.따라서 $n \ge 2^{h/2}-1$ 이고, $1$ 을 좌변으로 이항한 뒤 양쪽에 로그를 씌우면
$h \le 2lg(n+1)~~\blacksquare$
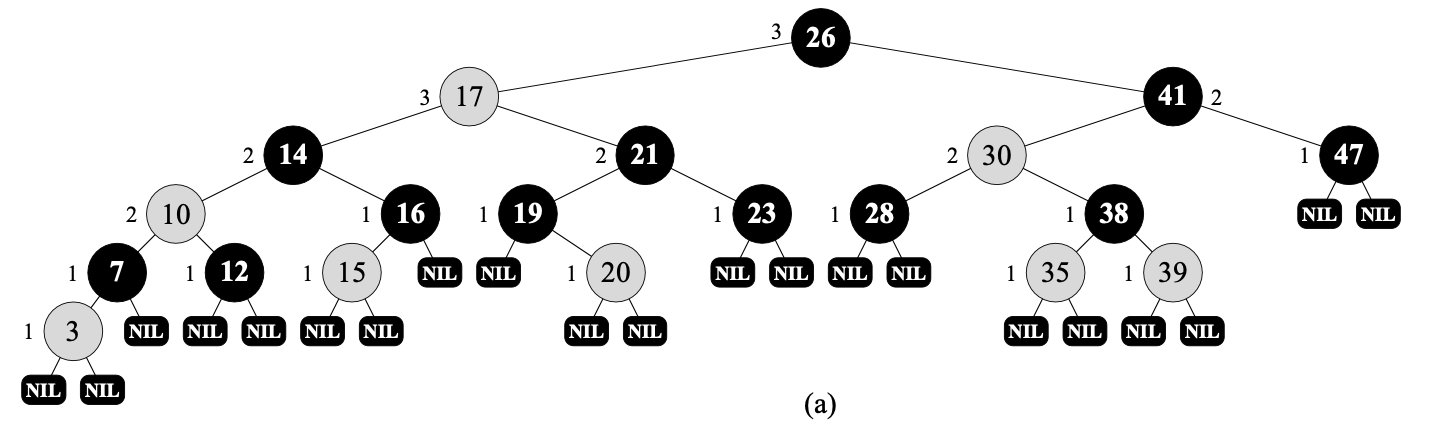
노드 옆의 숫자는 black-height 이며 검은색 노드가 black 노드, 회색 노드가 red 이다.
결국 높이의 상한이 있기 때문에, search, minimum, maximum, succcessor, predecessor operation은 $O(lgn)$ 이다. insert, delete 역시 $O(lgn)$ 의 시간 내에 할 수 있으며 방법은 밑에서 알아보자.
Rotations
Red-Black Tree의 성질을 유지하면서 insert, delete 를 하기 위해선 AVL 트리와 유사하게 회전이 필요하다. AVL 트리의 leftRotate, rightRotate 함수를 그대로 사용하지만 회전을 실행하는 조건을 다르게 주면 된다.
Insertion
RB Tree의 삽입은 BST와 같은 방법으로 삽입을 하며, 삽입된 노드를 red 로 설정하고 트리를 레드블랙 트리의 성질에 맞게 고쳐주면 된다. 삽입을 RBinsert , 고쳐주는 과정을 RBinsertFixup 라 하자.
RBinsert
insert는 단순히 BST 성질에 따라 삽입하고, 마지막에 z.color 를 설정한 뒤 트리 전체를 수정해주면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
RBinsert(T, z) //T는 트리, z 는 삽입할 노드
y = T.nil
x = T.root
while x != T.nil
y = x
if z.key < x.key
x = x.left
else x = x.right
z.p = y;
if y == T.nil
T.root = z;
else if z.key < y.key
y.left = z;
else y.right = z;
z.left = T.nil;
z.right = T.nil; //여기까진 BST와 같음!
z.color = RED;
RBinsertFixup(T, z)
RBinsertFixup
트리 전체를 Red-Black 트리에 맞게 수정하는 과정이 복잡한데, 일단 pseudo code를 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
RBinsertFixup(T, z)
while z.p.color == RED
if z.p == z.p.p.left
y = z.p.p.right
if y.color == RED //case 1: z의 uncle y가 red
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
else if z == z.p.right //case 2: z의 uncle y가 black 이고 z가 right child
z = z.p
leftRotate(T,z)
z.p.color = BLACK //case 3: z의 uncle y가 black 이고 z가 left child 인 경우
z.p.p.color = RED
rightRotate(T,z.p.p)
else //symmetric 하므로 right를 left로 바꾸면 됨
T.root.color = BLACK;//z가 root 노드였을 경우 red일테니 black로 바꿔준다.
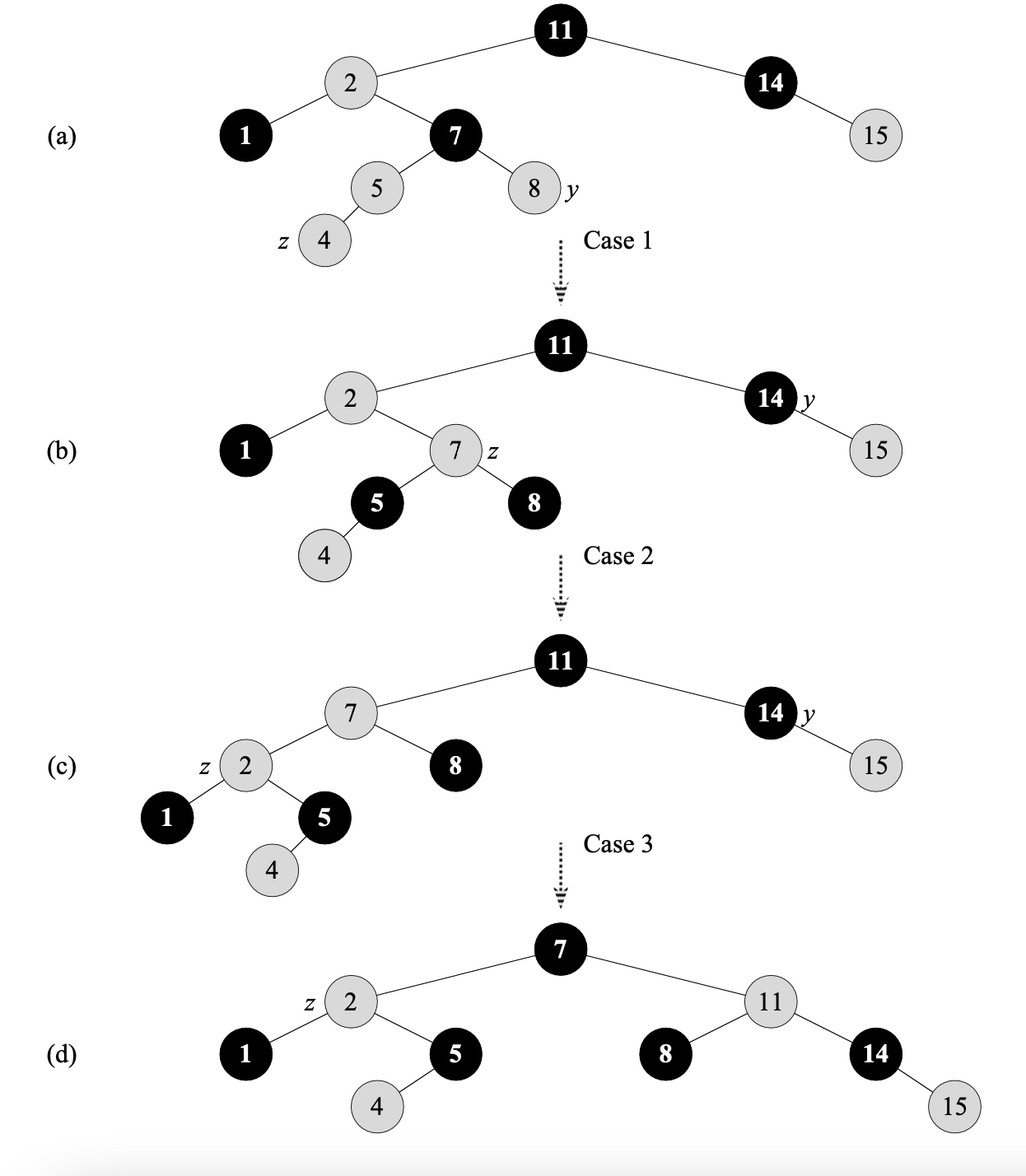
(a)는
z를 삽입한 직후이다. 새로운 노드를red로 삽입하여 _Property 4_를 위반하였고z의 uncle y가red이기 때문에 _case 1_이 된다. 코드를 진행하며color를 재설정 하고z의 위치를 옮기게 되어 (b)의 형태가 된다. 그리고 여전히z가red이므로 다시 반복문을 돈다.(b)에선
z와 부모노드가 둘 다red이고z의 uncle y가black이다.z가right child이므로 case 2 가 되어 코드가 진행되고, (c)의 결과가 나오며 다시 반복문을 진행한다.(c)에선 case 3 이 되어 코드가 진행된다. 이후엔 모두 레드블랙 트리의 성질을 만족하므로 끝난다.
코드의 while 문은 다음과 같은 성질이 유지되게(invariant) 해준다.
- 노드
z는red이다. - 만약
z.parent가root이면z.parent는black이다. - 만약 트리가 레드블랙 properties를 위반한다면, 최대 하나만 위반을 하고 위반한 property는 property 2 또는 property 4이다. 만약 property 2를 위반했다면,
z가root이며red인 경우이고, property 4를 위반했다면,z와z.parent둘 다red였기 때문이다. (property 1, 3, 5는 RBinsertFixup을 호출하기 전에 만족한 상태이다.)
반복문의 내용을 좀 더 자세히 살펴보자.
실제로 while 문에서 6개의 케이스를 다루어야 하지만 z.parent 가 z.parent.parent의 leftchild인지 rightchild 인지에 따라 3가지 / 3가지로 나뉘고, 이때 좌우가 완전히 대칭된 형태라서 3가지 케이스를 다룬 뒤 좌우를 모두 바꾸면 된다. (line 2가 분기점이 된다.) 이때 z 를 red 로 삽입하였고, z.parent가 red 인 경우에만 반복문에 들어오므로, 항상 z.parent.parent가 존재한다.(원래는 RB properties를 모두 만족했었으므로 부모노드가 red면 이는 root 노드일 수 없고 따라서 parent가 존재한다!)
uncle을 고려하는 이유: 현재 노드와 부모 노드가 모두 red이면 현재 노드가 black로 바뀌던지, 부모 노드가 black로 바뀌고 조부모 노드가 red이면 되는데, 조부모 노드가 red라면 RB Tree property 4에 의해 uncle노드를 고려해야 하기 때문!!
Case 1: z의 uncle y가 red
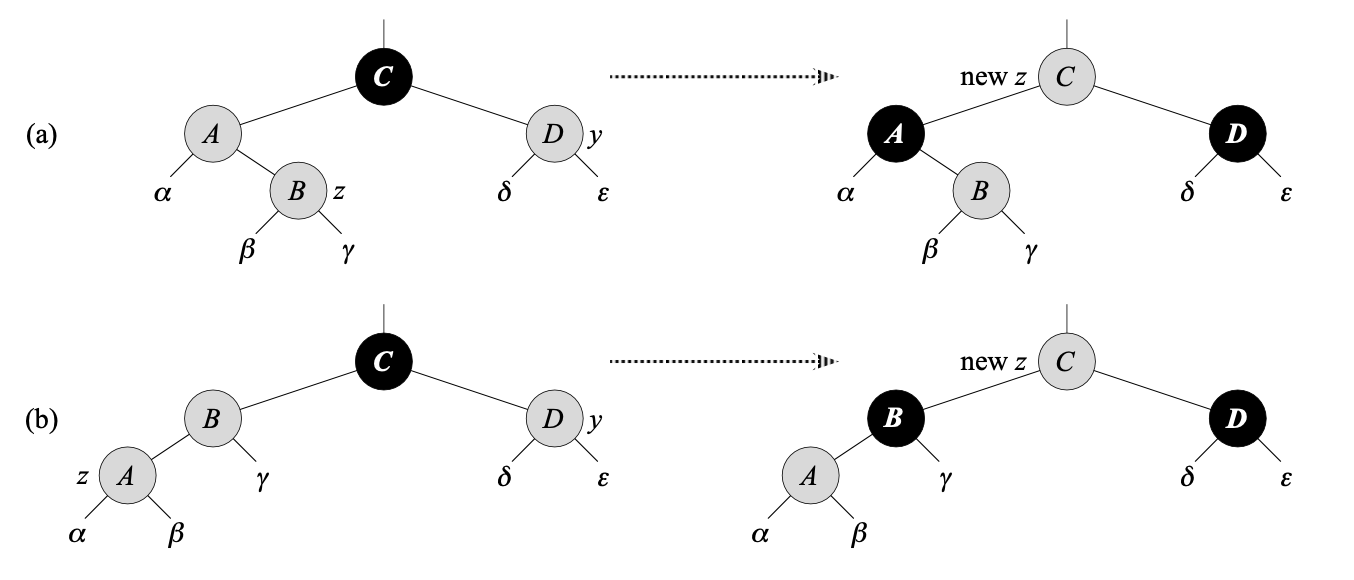
z와z.parent가 둘 다red로 property 4를 위반했다. (a), (b) 상황에서 같은 논리를 통해 이를 해결 할 수 있다. $\alpha, \beta, \gamma, \delta, \epsilon$ 는 subtree이며 모두 같은 black-height를 갖고 있다(property 5). Case 1의 코드는 몇몇 노드의 색깔을 property 5의 성질을 유지하면서 바꿔준다. 그리고z.parent.parent를 새로운z인z'로 한다. 그러면 property 4의 위반은 이z'에서만 발생 할 수 있다.
결국 다른 모든 레드블랙 트리의 성질을 유지한 채, 새로운 z에서 반복문을 실행하게 되어 불변성(invariant) 를 유지할 수 있다.
만약 z'가 root라면, property 2 만 위반된 상태로 반복문이 종료되고 이는 z' 때문이므로 색깔만 바꿔주면 된다.
만약 z'가 root가 아니고 z'.p 가 black 이면 아무런 위반도 없고 z'.p 가 red라면 다시 반복문을 수행한다.
Case 2: z의 uncle y가 black 이고 z가 right child
z.parent 에서 leftRotate를 하면 Case 3이 된다. 이때 z, z.parent 둘 다 red 이기 때문에 회전이 black-height나 property 5에 아무런 영향을 주지 않는다.
Case 3: z의 uncle y가 black 이고 z가 left child

color를 고려하며 회전을 하기 때문에 property 5를 위반하지 않으며, Case 3이 끝난 후 반복문이 종료된다.
Case 3에서는 색깔을 바꿔주고 회전을 하기 때문에 property 5를 유지할 수 있고 회전 후 연속된 두 노드가 red인 경우가 사라지며 z.parent가 black가 되기 때문에 반복문이 더이상 진행이 안되고 끝난다.
Analysis
RBinsert의 러닝타임을 계산해보자. n개의 노드를 가진 레드블랙 트리의 height는 $O(lgn)$ 이기 때문에, RBinsert에서 RBinsertFixup을 호출하기 전까지 $O(lgn)$ 이다. RBinsertFixup는 Case 1에서만 반복이 되며, z가 트리에서 2레벨씩 올라가기 때문에 $O(lgn)$이 된다. 따라서 전체 RBinsert의 러닝타임은 $O(lgn)$이 되고, Case 2나 3의 경우엔 반복문이 진행되지 않아 더 빨리 끝나게 된다.
삭제의 경우 다음 글에서 살펴보자.
Code(c)
이번에도 역시 코드가 너무 길어져서 헤더파일 / 틀 / 삽입 / 회전 으로 나누었다.
헤더파일
트리 노드를 위한 구조체와 컬러를 위한 enum 을 선언하였다. RED, BLACK에 자동으로 0과 1로 할당이 되었고, 임의의 값을 줄 수도 있다고 한다. 그냥 %d로 프린트를 하면 0과 1로 출력되지만(원본은 unsigned int라고 한다), 흥미롭게도 lldb에서 변수 명을 보면 RED, BLACK 이렇게 문자 그대로 출력된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#ifndef RBT_H
# define RBT_H
# include <stdio.h>
# include <stdlib.h>
# include <time.h>
typedef enum e_Color{
RED,
BLACK
} t_Color;
typedef struct s_rbt{
int key;
t_Color color;
struct s_rbt *parent;
struct s_rbt *left;
struct s_rbt *right;
} t_rbt;
t_rbt **initRBDeletion(t_rbt **root, t_rbt *nil, int key);
t_rbt **RBinsert(t_rbt **root,t_rbt *nil, int key);
void rightRotate(t_rbt **root, t_rbt *nil);
void leftRotate(t_rbt **root, t_rbt *nil);
#endif
메인 소스
nil 구조체와 main 함수, 출력, free 함수 파일이며 free 는 이번에도 후위 순회를 통해 하였고 leaks 를 통해 누수가 없음을 확인하였다. 주석 부분은 이 게시글의 첫번째 그림과 같은 트리를 만들어 비교하기 위해 썼던 데이터이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include "rbt.h"
t_rbt *makeNil(t_rbt *nil)
{
nil->parent = NULL;
nil->left = NULL;
nil->right = NULL;
nil->key = 0;
nil->color = BLACK;
return (nil);
}
void inOrdertoPrint(t_rbt *tree, t_rbt *nil)
{
if (tree != nil)
{
inOrdertoPrint(tree->left, nil);
printf("key : %d, color : %d\n", tree->key, tree->color);
inOrdertoPrint(tree->right, nil);
}
}
void postOrdertoFree(t_rbt *tree,t_rbt *nil)
{
if (tree != nil)
{
postOrdertoFree(tree->left, nil);
postOrdertoFree(tree->right, nil);
free(tree);
}
}
int main(void)
{
t_rbt **root;
t_rbt *nil;
int i;
int j = 0;
nil = (t_rbt*)malloc(sizeof(t_rbt));
nil = makeNil(nil);
root = (t_rbt**)malloc(sizeof(t_rbt*));
*root = nil;
srand(42);
// int a[20]={26,17,41,14,21,30,47,10,16,19,23,28,38,7,12,15,20,35,39,3};
while (j < 100)
{
i = rand() % 20000 + 1;
// RBinsert(root, nil, a[j]);
RBinsert(root, nil, i);
j++;
}
RBinsert(root, nil, 4242);
while ((*root)->parent != nil)
*root = (*root)->parent;
inOrdertoPrint(*root, nil);
postOrdertoFree(*root, nil);
free(root);
free(nil);
}
삽입 부분
BST, AVL Tree와 거의 동일한 방법으로 삽입을 하였으며 이전과 달리 color 를 고려해야 하므로 새로운 노드는 일단 RED 컬러를 할당한 뒤 RBinsertFixup 에서 레드블랙 트리 구조로 변환하였다. 이때 구조를 변화 시키면서 root노드가 바뀌는 경우, 함수가 끝나고 main함수로 갔을 때 root를 가리키지 않는 경우가 생겼는데, RBinsert 함수에서 root 조건체크를 수행하고 return 해주는 방식으로 해결하였다.
변수명을 깔끔하게 적고 싶었으나 디버깅 하면서 너무 헷갈려서 교재와 동일하게 맞추었다…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include "rbt.h"
void initNode(t_rbt *newnode, t_rbt *nil, int key)
{
newnode->parent = nil;
newnode->left = nil;
newnode->right = nil;
newnode->key = key;
}
void RBinsertFixup(t_rbt **newnode, t_rbt *nil)
{
t_rbt *y;
t_rbt *z;
z = *newnode;
while (z->parent->color == RED)
{
if (z->parent == z->parent->parent->left) //부모 노드가 left인경우
{
y = z->parent->parent->right; //y 는 uncle
if (y->color == RED) //Case 1.
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else //case 2, 3
{
if (z == z->parent->right) //case 2
{
z = z->parent;
leftRotate(&z, nil);
}
z->parent->color = BLACK; // case 3
z->parent->parent->color = RED;
rightRotate(&z->parent->parent, nil);
}
}
else //부모 노드가 right인 경우. symmetric한 구조라서 좌우만 바꾸면 됨
{
y = z->parent->parent->left;
if (y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
if (z == z->parent->left)
{
z = z->parent;
rightRotate(&z, nil);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
leftRotate(&z->parent->parent, nil);
}
}
}
if (z->parent == nil) //이때는 root 노드가 된다.
z->color = BLACK;
}
t_rbt **RBinsert(t_rbt **root,t_rbt *nil, int key)
{
t_rbt *y;
t_rbt *x;
t_rbt *newnode;
newnode = (t_rbt*)malloc(sizeof(t_rbt));
initNode(newnode, nil, key);
y = nil;
x = *root;
while (x != nil)
{
y = x;
if (key < x->key)
x = x->left;
else x = x->right;
}
newnode->parent = y;
if (y == nil)
*root = newnode;
else if (key < y->key)
y->left = newnode;
else y->right = newnode;
newnode->color = RED;
RBinsertFixup(&newnode, nil);
if((*root)->parent != nil)
(*root) = (*root)->parent;;
return (root);
}
회전
AVL Tree의 회전 부분이랑 동일하다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include "rbt.h"
void leftRotate(t_rbt **rbt, t_rbt *nil)
{
t_rbt *x;
t_rbt *y;
x = *rbt;
y = x->right;
x->right = y->left;
if (y->left != nil)
y->left->parent = x;
if (x->parent == nil)
y->parent = nil;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->parent = x->parent;
y->left = x;
x->parent = y;
}
void rightRotate(t_rbt **rbt, t_rbt *nil)
{
t_rbt *x;
t_rbt *y;
x = *rbt;
y = x->left;
x->left = y->right;
if (y->right != nil)
y->right->parent = x;
if (x->parent == nil)
y->parent = nil;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->parent = x->parent;
y->right = x;
x->parent = y;
}
전체 코드는 깃허브에서 볼 수 있으며 make 명령어를 통해 컴파일해서 확인할 수 있다. (Unix환경에서 gcc 컴파일러를 사용했습니다.)
삽질🤦
무슨일인지 모르겠지만, 중위순회시 순서가 꼬이는 오류가 발생하였다. BST와 동일한 알고리즘을 사용했기에 오름차순으로 값이 나와야 하는데 중간에 이상한 값이 들어 있었고 색깔도 다 꼬여있었다. 단순 삽입에는 문제가 없었으니 Rotation 부분이 에러인것 같다. pseudo code 보면서 완전히 이해했다고 생각했는데 왜지??? lldb를 열심히 돌려본 결과, RBinsert에 들어오는 root 노드가 RBinsertFixup과정에서 바뀌게 되면 반영되지 않는다는점이 문제란 것을 알아냈다.
값은 잘 정렬되어 나오는데 책의 그림과 같은 예시를 넣어 봤는데 color가 달라서 당황했지만, 생각해보니 정렬되어 나왔다는 것이 목적에 이미 부합한 것이고 트리는 값을 넣는 순서에 따라 구조가 조금씩 달라질 수 있다는 것이 생각나서 납득하였다. 그래서 책의 그림과 똑같이 나오도록 삽입 순서를 잡아주니 색깔까지 똑같은 답이 나왔다!
AVL에서도 느꼈지만, 트리와 회전 개념이 들어가다 보니 포인터가 살짝만 꼬여도 디버깅하는데 오래 걸리고 자식노드와 부모노드 양 방향에서 서로를 가리키게 하다 보니 실수도 잦았다. 만들어놓고 쓰는게 아닌 이상 그때그때 이런 코드를 짜서 쓰는건 힘들것 같다…
참조
Introduce to Algorithms, 3rd Edition
modfied:27 Apr 2021
Comments