MIT introduction to Algorithm (6.006) Lecture 7을 기반으로 정리한 내용입니다.
데이터를 비교 및 정렬하는 알고리즘을 위한 ADT를 살펴보고, 각 알고리즘의 Lower Bound를 살펴보자. 그리고 적은 양의 정수로 이루어진 데이터에 대하여, $O(n)$ 의 시간복잡도를 지니는 계수 정렬과 기수 정렬에 대해 살펴보자.
힙 정렬, 병합 정렬이나 퀵 정렬은 흔히 사용되며 $\Omega(nlgn)$ 의 시간복잡도를 가진다. 이런 정렬들은 공통적인 특징을 가지는데, 바로 입력된 두 데이터를 비교하면서 정렬을 한다는 것이다. 이런 정렬 알고리즘을 Comparison Sorts라고 하자. 이 게시글에서 어떤 Comprision Sorts라도 최악의 경우 $\Omega(nlgn)$ 의 시간복잡도를 지닌다는 것을 증명할 것이다.
Decision Tree(의사 결정 트리)
Comprision Sort 알고리즘은 의사 결정 트리로 나타낼 수 있으며, 의사 결정 트리는 모든 데이터와 특정한 값 n을 비교하여 결과를 낼 수 있다. 예를 들어, 3개의 원소에 대한$(n = 3)$ 의사 결정 트리는 다음과 같이 구성된다.
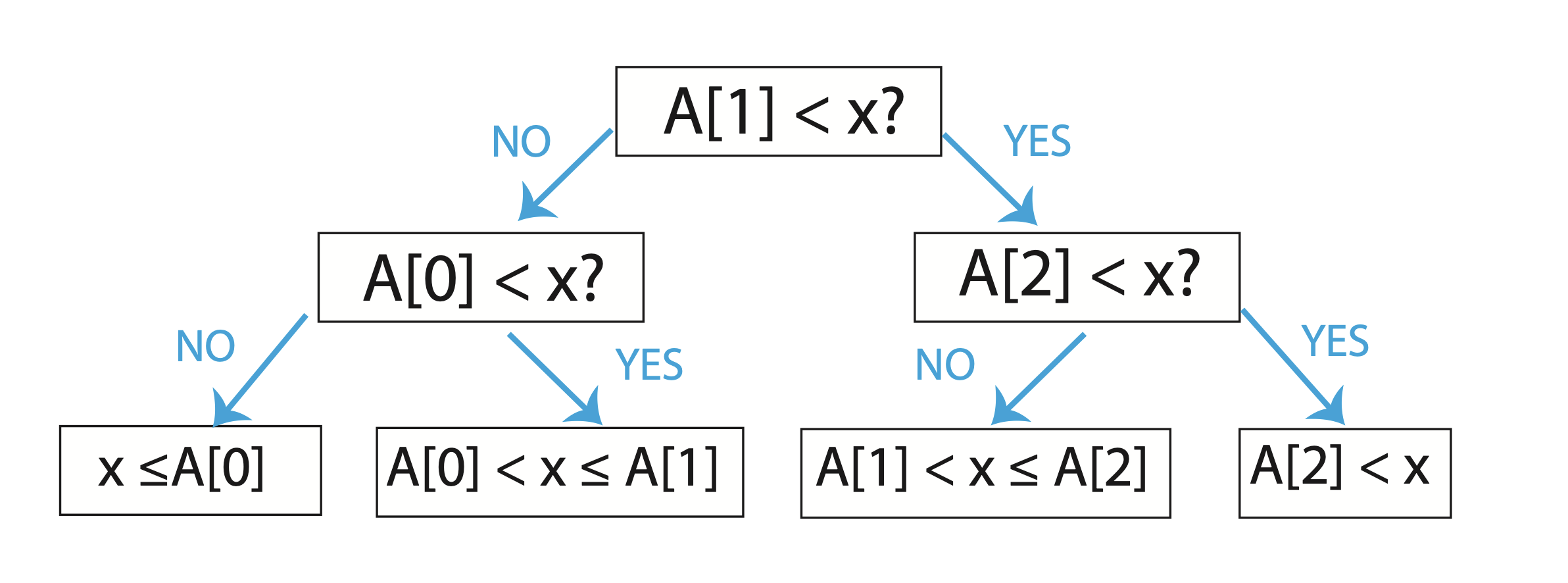
x는 새로운 데이터이고, A[]는 입력 되어 있던 데이터라고 하자. 그림과 같이 트리의 구조로 탐색을 할 수 있으며 각 leaf는 모든 데이터와 대소 비교 한 결과가 된다.
Lower Bound
탐색의 Lower Bound
n개의 데이터가 이미 정렬되어 있을 때 어떤 데이터 x를 찾는 알고리즘은 $\Omega(lgn)$ 이 된다.(Lower Bound = $lgn$)
간단한 증명(?)
n개의 데이터가 정렬되어 있으면, n개의 노드를 가진 의사 결정 트리가 되고, 트리의 leaf를 찾아가야 하므로 트리의 높이만큼의 시간이 걸릴 것이다. 의사 결정 트리는 이진 트리 이므로 높이는 $lgn$ 이 된다.
정렬의 Lower Bound
세개의 데이터를 정렬하는 의사 결정 트리는 조금 더 복잡하게 생겼는데, 3가지 원소{1, 2, 3}을 정렬하는 경우 다음과 같은 트리를 이용하여 경우의 수 들을 찾을 수 있다.

이와 같이 모든 경우의 수를 고려한다면 하나의 순열이 되므로 $n!$ 이 되며 여기서는 3개의 원소가 있으므로 $3!$ 개가 나온다.
결국 $n!$개의 데이터를 갖는 하나의 트리로 생각할 수 있으며 $height \ge lg(n!)$ 가 된다. 이를 로그의 성질에 따라 잘 분해한 뒤 계산하면 $\Omega(nlgn)$ (=Lower Bound)가 된다.
증명)
스털링 근사 $n! \sim \sqrt{2\pi n}(n/e)^n$ 을 이용하면 더 깔끔하지만, 이에 대해 제대로 배운 적이 없으니 다른 방법으로 증명한다…
$lg(n!)$
$=lg1+lg2+…+lg(n-1)+lg(n)$ (로그의 성질)
$=\sum_\limits{i=1}^\limits{n}lg(i) ~ (where ~i = integer)$
(시그마 표현으로 전환)
$\ge \sum_\limits{i=n/2}^\limits{n}lg(i)$
(로그이므로 모든 수는 양수이므로 $i=1 \sim n$ 까지 더하는 것 보다 $n/2 \sim n$ 까지 더하는게 작다)
$\ge \sum_\limits{i=n/2}^\limits{n}lg(n/2) = \sum_\limits{i=n/2}^\limits{n}(lg(n)-1)$
(로그는 단조증가함수 이므로 $lg(n/2) + lg(n/2 + 1) + … + lg(n) \ge lg(n/2) + lg(n/2) + … +lg(n/2)$) 이고, $lg(n/2)$ 을 로그의 성질에 따라 풀어서 쓰면 우변의 식이 나온다)
$\sum_\limits{i=n/2}^\limits{n}(lg(n)-1) = n/2 * lg(n) - n/2$ 이고, $lg(n!)$ 가 항상 이 값보다 크므로
$\Omega(nlgn) \blacksquare$
이렇게 정렬은 최소한 $nlgn$ 의 시간복잡도를 갖지만, 데이터의 수가 너무 많지 않고 (not too big) 모두 $integer$ 라는 가정 하에 $O(n)$ 시간 내에 정렬을 수행 할 수 있는 알고리즘이 있다. 이에 대해 알아보자.
Linear Time Sort
Counting Sort (계수 정렬)
계수 정렬은 세개의 배열을 필요로 하는데, 원본 데이터를 갖고 있는 A[1...n] 와 정렬된 결과를 나타낼 B[1...n] 그리고 정렬을 위해 임시로 값을 저장할 C[0...k] 가 필요하다. 이때 원본 데이터는 0부터 k사이의 숫자여야 한다. (계수 정렬의 가정!!) 이러한 성질을 갖는 데이터가 있다면, 원본 데이터를 C[] 의 인덱스로 하고 C[] 의 값에 각 인덱스에 해당하는 데이터의 개수를 저장한 후 B[]에 순서대로 넣으면 성공적으로 정렬 된다는 논리로 진행된다. Pseudo Code와 그림을 통해 이해해보자.
Pesudo Code
1
2
3
4
5
6
7
8
9
10
11
Counting-Sort(A, B, k)
C[k] //C를 정의
for i = 0 to k //C 초기화
C[i] = 0
for j = 1 to A.length //C의 A[j]번째 인덱스마다 한번씩 ++ 해줌
C[A[j]]++ //C[i]는 i값을 가지는 데이터가 몇 개 있는지 저장함
for i = 1 to k
C[i] = C[i] + C[i-1] // C[i]는 이제 i보다 같거나 작은 데이터들의 수를 저장함
for j = A.length downto 1 //마지막 반복문은 밑에서 설명한다.
B[C[A[j]]] = A[j]
C[A[j]] = C[A[j]] - 1
Line 7 ~ 8 은 C[]가 점점 증가하는 모습의 배열로 만드는데, 이렇게 만들게 되면 C[i-1] == C[i] 일때는 i라는 데이터가 없다는 의미가 되고, C[i] - C[i-1] = 2 라면 i라는 데이터가 2개 있다는 뜻이 된다. 또한 C[i]에 저장된 값은 데이터가 정렬되었을때, 그 i값이 C[i]번째에 들어가면 정렬이 된다는 뜻이 된다.
Line 9 ~ 11의 반복문은 A[] 의 각 원소들을 B[] 에 올바르게 정렬하여 넣어준다.
만약 A[]에 있는 모든 n(=A.length)개의 원소들이 중복되지 않는다면(distinct 하다면), Line 11은 고려할 필요 없이 C[]에 저장된 형태에 따라 정렬된 데이터가 B[] 의 배열로 나타날 것이다.
하지만 이 원소들이 중복될 수 있기 때문에 C[A[j]]을 매번 감소시키며 A[j]의 값을 B[j]에 넣는다. C[i]은 i데이터가 정렬된 자리를 뜻하고, 이를 감소시키면 이전 i 자리보다 한 칸 앞자리에 해당하는 값이 C[i]에 들어간다. 이때 i데이터가 여러 개 있어서 다시 C[i]자리를 거치게 된다면, 이전 i의 앞자리에 같은 i가 들어가서 정렬되는 것이다.
글로 설명하니 상당히 난잡한데 A, B, C를 코드에 따라 하나씩 그려보면서 이해하면 깔끔하게 이해가 된다…!
다음은 A[1...8] 에 대해 계수 정렬을 하는 과정이다. A의 원소는 모두 5보다 같거나 작은 양의 정수이다.(즉 k = 5 이다.)
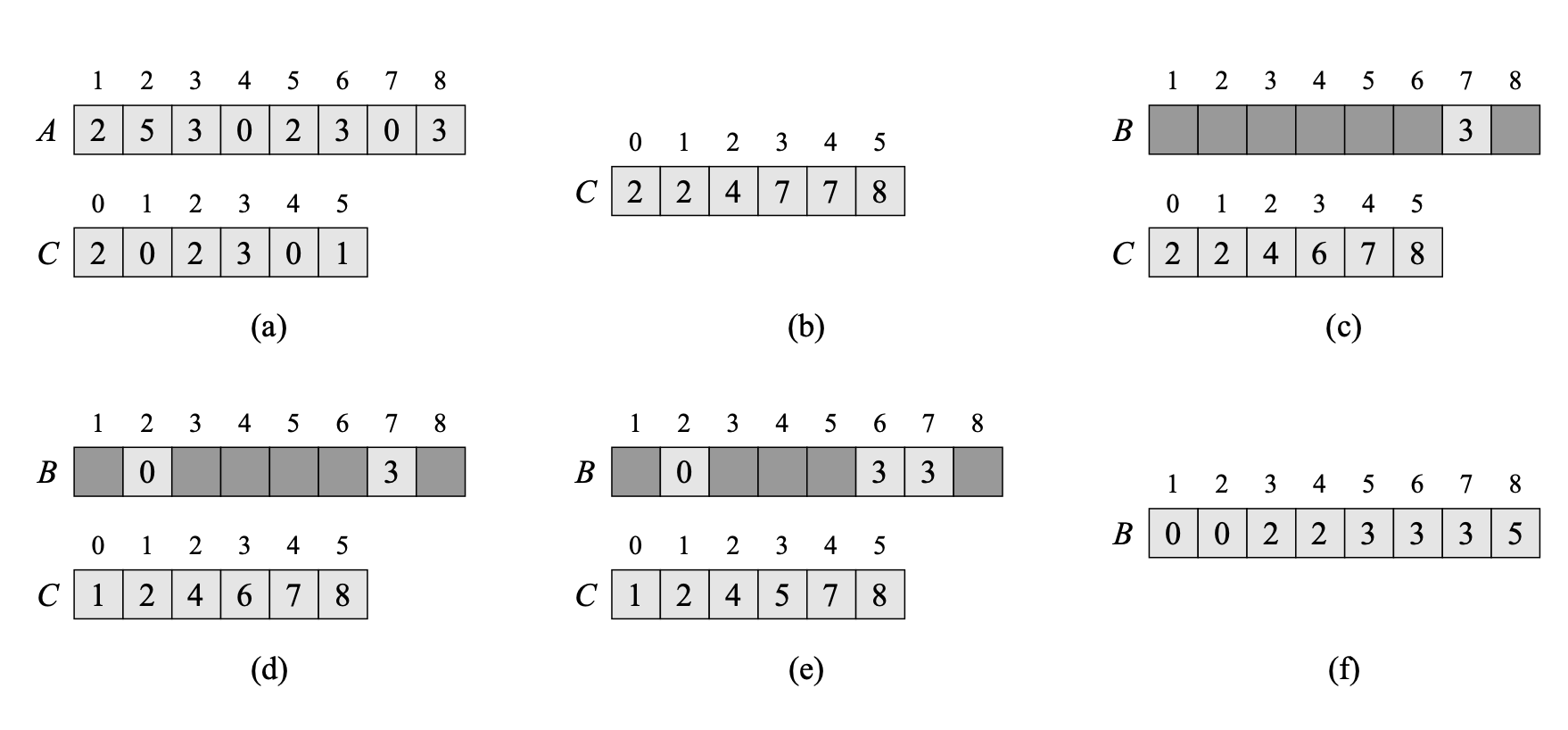
(a) Line 6 이후 배열
A[]와C[]의 모습이다. 0이 2개 있어서C[0] = 2, 1이 0개 있으니C[1] = 0, 3이 3개 있으니C[3] = 3이 되는 구조이다.(b) Line 8 이후 배열
C[]의 모습이다. 피보나치 수열처럼 현재 값 + 이전 값이 다음 위치에 들어간다. 이 배열C[]만 보고도C[0] == C[1]이니 1이란 데이터는 없다는 것을 알 수 있고C[3] - C[2] == 3이라는 점에서 3이 3개 있으며, 7번째 자리까지 3이 들어갈 것 이라는 사실을 도출해 낼 수 있다.(c) ~ (e) Line 9 ~ 11을 3번 반복하는 B와 C의 모습이다. 진한 회색으로 표시된 부분은 아직 값이 삽입되지 않은 부분이다.
(f)는 반복문을 마치고 정렬된 결과인 B를 나타낸다.
Analysis
Line 3 ~ 4에 해당하는 반복문은 $\Theta(k)$ 의 시간이 걸리고, Line 5 ~ 6은 $\Theta(n)$, Line 7 ~ 8 은 $\Theta(k)$, 마지막으로 Line 9 ~ 11 은 $\Theta(n)$ 의 시간이 걸린다. 따라서 전체 시간복잡도는 $\Theta(k + n)$ 이 되는데, 계수 정렬에서 보통 $k = O(n)$ 정도로 하기 때문에 $\Theta(n)$ 의 시간복잡도를 가진다고 본다. (또한, $\Theta(k + n)$ 의 공간을 필요로 한다.)
Code(C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<stdio.h>
#include<stdlib.h>
#define SIZE 42 // n과 같음
#define MAX_VALUE 21 //k와 같음
//origin = A, sorted = B, tmp = C
int *countingSort(int *origin, int *sorted)
{
int tmp[MAX_VALUE];
int i;
int j;
i = 0;
j = 1;
while (i < MAX_VALUE)
{
tmp[i] = 0;
i++;
}
while (j < SIZE)
{
tmp[origin[j]]++;
j++;
}
i = 1;
while (i < MAX_VALUE)
{
tmp[i] = tmp[i] + tmp[i-1];
i++;
}
while (0 < j)
{
sorted[tmp[origin[j]]] = origin[j];
tmp[origin[j]] = tmp[origin[j]] - 1;
j--;
}
return (sorted);
}
int main(void)
{
int *origin;
int *sorted;
int i;
i = 1;
sorted = (int*)malloc(sizeof(int)*SIZE);
if (sorted == NULL)
return 1;
origin = (int*)malloc(sizeof(int)*SIZE);
if (origin == NULL)
return 1;
srand(42);
while (i < SIZE)
{
origin[i] = rand()%MAX_VALUE;
printf("%dth origin data is %d\n", i, origin[i]);
i++;
}
sorted = countingSort(origin, sorted);
i = 1;
while (i < SIZE)
{
printf("%dth sorted data is %d\n", i, sorted[i]);
i++;
}
free(sorted);
free(origin);
}
Radix Sort (기수정렬)
기수 정렬은 상당히 직관적인데, 만약 d자리의 수가 있다면 각 숫자의 가장 끝자리부터 첫째 자리 까지 순차적으로 정렬을 하는 알고리즘이다. 예를 들어 3자리 수를 정렬한다면 다음 그림과 같다.
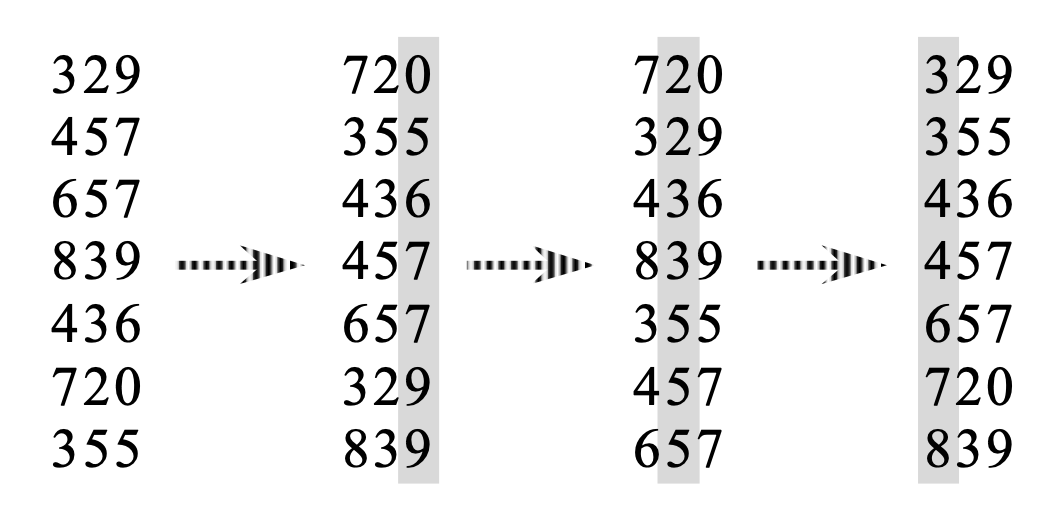
또한 10진수 뿐만 아니라 임의의 b 진법으로 이루어진 데이터를 정렬할 수 있는데, b 진법 수인 k의 자릿수 d는 $d=log_bk$가 되며, 각 자릿수는 0부터 b-1까지의 수여야 한다.
이런 기수 정렬은 주로 여러개의 field로 구성된 키들을 정렬할때 쓰는데 대표적으로 연-월-일 순으로 정렬할 때 사용한다.
Pseudo Code
1
2
3
Radix-Sort(A, d)
for i = 1 to d
use a stable sort to sort array A on digit i
Pseudocode 역시 매우 간단한데, 각 자릿수에 대해 적절한 정렬 알고리즘을 수행해주면 된다. 이때 각 자릿수는 k보다 작고(10진수면 0~9까지), 전체 n개의 수가 있을 수 있으니 계수 정렬(Counting Sort)의 조건과 완벽하게 부합한다.
따라서 시간 복잡도 역시 $\Theta(d*(n+k))$ 가 되며, $d$가 상수이고 $k = O(n)$ 이라면 기수 정렬을 선형 시간 내에 수행할 수 있다.
b 진법일때 시간복잡도도 공부하기……. 기억이 안난다…. 증명이 안된다………
Code (C)
삽질🤦♂️
Radix Sort… 배열로 처리하려고 맘먹고 코드를 짜는데 수많은 문제에 부딪혔다…….. 일단 자릿수별로 뽑아서 비교를 한 뒤 원본 배열을 이리 저리 비교하면서 정렬해야 하는데 원본을 유지하면서 자릿수만 뽑는게 문제였다. 자릿수만 뽑아서 정렬하면 아무 의미가 없고 원본 데이터를 조작하면 그때그때 백업을 해 놓아야 하니 너무 찝찝했다.
적당히 나누기와 모듈러 연산을 통해 기가막힌 방법을 찾아 컴파일 하였으나 냉정한 터미널은 segmentation fault란 답을 줬다. Origin[j] / digit % MAX_VALUE * digit로 했으나, 몫은 자릿수까지 버린다는 사실을 간과했었고, 그래서 그냥 %MAX_VALUE 로 해결하였다.
CountingSort함수를 그대로 활용하였더니 첫 자리만 정렬된 결과가 나왔다. 대체 왜????????????????????
modfied:02 May 2021
Comments